Иллюстрированный самоучитель по Visual Studio.Net
Контейнер точек
Зададимся целью нарисовать в логической системе координат плоский многоугольник (Polygon), координаты точек которого будем хранить в динамической структуре данных. Специалисты советуют в таких случаях пользоваться одним из множества шаблонов, реализующих поведение фундаментальных структур данных и присутствующих в рамках STL (Standard Template Library). Библиотека шаблонов STL доступна на любой платформе, так как является стандартом. Она станет доступной и нам, если мы подключим необходимый файл заголовков. Для хранения точек многоугольника мы выберем шаблон стандартного контейнера, который называется vector. Это динамическая структура данных, которая ведет себя как «умный» массив элементов произвольного типа. Любой контейнер удобно представлять себе в виде резиновой сумки с одинаковыми объектами любой природы, которая почти всегда полна и в которую всегда можно положить еще разумное количество объектов того же типа. Это возможно, потому что она растягивается, то есть способна динамически (на этапе выполнения) изменять свои размеры как в сторону увеличения, так и в сторону уменьшения.
Подробнее о контейнерах будет сказано позже, а сейчас надо решить, что должно в нем храниться. Так как многоугольник определяется координатами точек, то контейнер целесообразно «скроить» (по шаблону vector) так, чтобы в нем можно было хранить объекты класса CPoint. Этот класс является вспомогательным в MFC (не происходит от CObject). Найдите этот класс в иерархии классов библиотеки MFC. Для этого:
Класс CPoint находится в правой части карты под заголовком Simple Value Types. После этого отыщите классы: CObject, CDocument, cview, cwnd, которые так или иначе присутствуют в каркасе нашего приложения. Закройте окна Index, Index Results и Hierarchy Chart.
Теперь вы знаете, что CPoint содержит внутри себя две целые координаты (х, у) произвольной точки и множество полезных методов для управления точкой. Итак, мы решили хранить точки многоугольника (объекты класса CPoint) в контейнере, скроенном по шаблону vector<CPoint>. Параметр шаблона (в угловых скобках) указывает тип объектов, которые будут храниться в контейнере. Воспользуемся контекстным меню, возникающим при правом щелчке мыши (right-click) на имени класса CMyDoc в окне Class View. В этом меню:
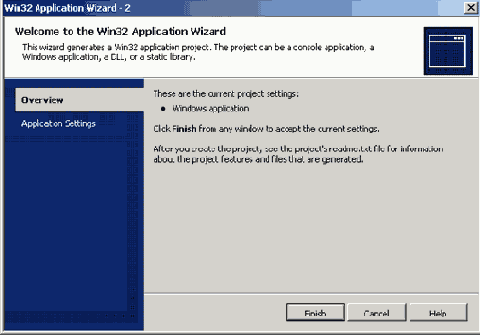

Рис. 1.5. Окно мастера Add Variable
Просмотрите описание класса CMyDoc, дважды щелкнув на имени класса в окне Class View. В конце файла вы должны увидеть строку
vector<CPoint> m Points;
Теперь просмотрите тело конструктора класса. Для этого раскройте элемент дерева CMyDoc и дважды щелкните на имени конструктора CMyDoc (void). Вы должны увидеть такой заголовок и тело конструктора:
CMyDoc::CMyDoc()
: m Points (0)
{
}
Обратите внимание на инициализатор m_Points (0), который был автоматически вставлен мастером Add Variable. Инициализатор вызывает один из конструкторов шаблона классов vector и сообщает ему, что перед тем, как создать объект класса CMyDoc, надо создать объект m_Points типа vector и задать ему нулевой размер. Нам не нужен этот инициализатор, так как мы собираемся записать в контейнер m_Points координаты тестового многоугольника. Тело конструктора документа пока пусто. Наполним его кодами, вычисляющими точки многоугольника, так чтобы он имел вид пятиконечной звезды. Звезда удобна тем, что позволяет продемонстрировать способы закраски самопересекающихся многоугольников. Измените коды конструктора:
CMyDoc: : CMyDoc ()
//====== Вспомогательные переменные
double pi = 4 . * atari (1.),
al = pi / 10. , // Углы
a2 = 3. * al,
// ====== 2 характерные точки
x1 = cos (al) ,
yl = sin (al) ,
x2 = cos (a2) ,
y2 = sin(a2) ,
x[5], у [5];
//===== Вещественные (World) координаты углов звезды
//===== Считаем, что начало координат находится
//===== в геометрическом центре звезды
х [ 0 ] = 0 . ; у [ 0 ] = 1 . ; // Макушка звезды
х[1] = -х2; у[1] = -у2; // Нижний левый угол
х[2] = xl; У [2] = yl; // Верхний правый угол
х[3] = -xl; y[3] = yl; // Верхний левый угол
х[4] = х2; У [4] = -у2; // Нижний правый угол
//===== Логические координаты углов звезды
//===== запоминаем в контейнере
for (int i=0; i<5; i++)
//===== Точка в логической системе координат
// Увеличиваем в 100 раз, переводим в целые
// и сдвигаем
CPoint pt(200 + int(100. * x[i]), 150 - int(100. * y[i]));
//===== Записываем в конец контейнера
m_Points.push_back(pt);
}
}