§ 68. Общие сведения о метрических задачах
К метрическим относятся задачи, связанные с определением истинных (натуральных) величин расстояний, углов и плоских фигур на комплексном чертеже. Можно выделить три группы метрических задач.
1. Группа задач, включающих в себя определение расстояний от точки до другой точки; от точки до прямой; от точки до плоскости; от точки до поверхности; от прямой до другой прямой; от прямой до плоскости; от плоскости до плоскости. Причем расстояние от прямой до плоскости и между плоскостями измеряется в тех случаях, когда они параллельны.
2. Группа задач, включающая определение углов между пересекающимися или скрещивающимися прямыми, между прямой и плоскостью, между плоскостями (имеется в виду определение величины двухгранного угла).
3. Группа задач, связанная с определением истинной величины плоской фигуры и части поверхности (развертки).
Приведенные задачи могут быть решены с применением различных способов преобразования чертежа. В основе решения метрических задач лежит свойство прямоугольного проецирования, заключающееся в том, что любая геометрическая фигура на плоскость проекций проецируется в натуральную величину, если она лежит в плоскости, параллельной этой плоскости проекций. Решение задач значительно упрощается, если хотя бы одна из геометрических фигур, участвующих в задачах, занимает частное положение. Если одна из геометрических фигур не занимает частного положения, необходимо выполнить определенные построения, позволяющие провести одну из них в это положение.
§ 69. Определение истинной величины расстояний
Некоторые задачи на определение расстояний рассматривались в предыдущих разделах. Например, в § 42 определялась натуральная величина отрезка прямой линии методом треугольника, в § 57 определялась натуральная величина отрезка способом плоскопараллельного переноса. Эта задача может быть также решена способом замены плоскостей проекций (см. § 58) или способом вращения (см. § 59). Определение длины отрезка прямой позволяет решить задачу определения расстояния от точки до точки, так как это расстояние и определяется отрезком прямой. Расстояние от точки до прямой измеряется отрезком перпендикуляра, проведенного из точки к прямой. Отрезок этого перпендикуляра изображается в натуральную величину на плоскости в том случае, если он проведен к проецирующей прямой. Значит, нужно преобразовать чертеж данной прямой, сделав ее в новой системе плоскостей проекций проецирующей (см. § 58, задача 2). На рис. 140 определено расстояние от точки М до прямой АВ:
1) П2_|_П1-> П1_|_П4, П4 ||АВ, П1/П4 ||A1B1;
2) П1П4 -> П4_|_П5, П5 _|_AB, П4/П5 _|_A4B4;
3) M5K5 — истинное расстояние от точки М до прямой AB;
4) чтобы построить проекции перпендикуляра МК в исходной системе плоскостей, строят основание перпендикуляра— точку К—на прямой АВ из условия, что в системе П4 _|_П5; он занимает положение линии уровня, т. е.
M4K4_|_A4B4. Горизонтальная и фронтальная проекции точки К определяются по линиям из условия принадлежности ее прямой АВ. Расстояние от точки до плоскости измеряется отрезком перпендикуляра, опущенного из точки на плоскость. Так как перпендикуляр к проецирующей плоскости есть линия уровня, то удобно иметь на чертеже «вырожденную» проекцию данной плоскости, т. е. преобразовать чертеж (см. § 58, задача 3). На рис. 141 построены проекции перпендикуляра МК, отрезок которого определяет расстояние от точки М до плоскости Q(ABC):

Рис.
140
2) М4K4 _|_Q4 — истинная величина расстояний от точки М до плоскости Q;
3)M1K1_|_K4Kl или || П1/ П4;
4) K2 построена с помощью высоты точки К, измеренной на плоскости П4.
Расстояние
между параллельными прямыми измеряется отрезком перпендикуляра между ними. На
рис. 142 определено расстояние между прямыми а и b путем преобразования
чертежа прямых. Сначала построено

Рис.
141
а(b)|| П4; П1 /П4 ||а,(b1).
В системе плоскостей П4 _|_ П5 прямые занимают проецирующее по отношению к плоскости Пз положе-

Рис.
142
Для определения расстояния между скрещивающимися прямыми необходимо одну из прямых сделать проецирующей в новой системе плоскостей проекций.
Расстояние от прямой до плоскости, параллельной прямой, измеряется отрезком перпендикуляра, опущенного из любой точки прямой на плоскость. Значит, достаточно плоскость общего положения преобразовать в положение проецирующей плоскости, взять на прямой точку, и решение задачи будет сведено к определению расстояния от точки до плоскости.
Расстояние между параллельными плоскостями измеряется отрезком перпендикуляра между ними, который легко строится, если плоскости займут проецирующее положение в новой системе плоскостей проекции, т. е. опять используется третья исходная задача преобразования чертежа.
§ 70. Определение истинной величины углов
Задачу на определение истинной величины углов (плоских) удобнее решать путем преобразования исходного чертежа способом вращения вокруг линии уровня. Истинная величина углов между пересекающимися прямыми с и d (рис. 143) определена следующим образом: плоскость угла повернута вокруг своей фронтали f (1, 2) до совмещения ее с фронтальной плоскостью уровня Ф (Ф1), проходящей через

Рис.
143
Эта задача также может быть решена способом замены плоскостей проекций. Для этого двойной заменой плоскостей проекций нужно сделать плоскость угла плоскостью уровня, решив последовательно сначала третью исходную задачу, а затем — четвертую.
Натуральная величина угла между скрещивающимися прямыми определяется как угол между двумя пересекающимися прямыми, параллельными данным скрещивающимся прямым.
Угол а между прямой l и плоскостью 6 может быть определен через дополнительный угол р между заданной прямой l и перпендикуляром п к данной плоскости, проведенной из любой точки прямой (рис. 144). Угол Р дополняет искомый угол а до 90°. Определив истинную величину угла Р путем вращения вокруг прямой уровня плоскости угла, образованного прямой l и перпендикуляром и, остается дополнить его до прямого угла. Этот дополнительный угол и даст истинную величину угла а между прямой l и плоскостью 0.
Истинная величина двугранного угла — между двумя плоскостями Q и л. — может быть определена или путем замены плоскости проекций с целью преобразования ребра двугранного угла в проецирующую прямую (задачи 1 и 2), или если ребро не задано, как угол между двумя перпендикулярами n1 и n2, проведенными к данным плоскостям (см. § 61) из произвольной точки М пространства (см. рис. 145). В плоскости этих перпендикуляров при точке М получаем два плоских
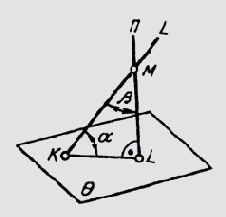
Рис. 144

Рис.
145
§ 71. Определение истинной величины плоской фигуры
Определение истинной величины плоской фигуры можно осуществить путем преобразования чертежа способом замены плоскостей проекций. На рис. 146, а дан комплексный чертеж прямоугольника ABCD. Ни одна из проекций прямоугольника не занимает частного положения. Задачу решаем последовательным решением третьей и четвертой основных задач. Заменив плоскость П2 на П4, приводим прямоугольник в частное положение, т. е. в виде проецирующей по отношению к П4- Выполнив вторую замену, то есть замену П4 на П5, определяем истинную величину прямоугольника ABC.
Задачу определения истинной величины прямоугольника можно также решить способом вращения вокруг линии уровня плоскости этой фигуры до совмещения с соответствующей плоскостью уровня (рис. 146, б).
В ряду рассматриваемых задач может быть также решена задача на определение истинной величины фигуры сечения поверхности проецирующей плоскостью. В этом случае достаточно одной замены плоскостей проекций (исходная задача 3). В этом случае истинную величину фигуры сечения можно легко построить путем непосредственного замера расстояний точек фигуры «вдоль сечения» и «поперек сечения» (рис. 147).
Длина фигуры сечения АВ изображается в истинную величину на плоскости П2, так как является отрезком фигуры фронтали секущей плоскости. Расстояние между симметричными точками «поперек сечения» изображается в натуральную величину на плоскости П1 так как является отрезками горизонталей секущей плоскости Sum.
§ 72. Построение разверток поверхностей
При изготовлении различных конструкций и изделий из листового материала имеет большое значение построение разверток поверхностей. Если представить себе поверхность как гибкую нерастяжимую пленку, то некоторые из них путем изгиба можно совместить с плоскостью без разрывов и деформаций. Такие поверхности относятся к развертывающимся, а полученную в результате развертывания поверхности плоскую фигуру называют разверткой этой фигуры. Те поверхности, которые нельзя совместить без разрывов и деформаций, относятся к неразвертываемым (см. § 45).
В практике возникает необходимость изготовления из листового железа не только развертывающихся плоскостей. Теоретически точно развертываются только гранные поверхности, торсы, конические или цилиндрические поверхности. При развертывании конических и цилиндрических поверхностей общего вида в практике их аппроксимируют вписанными гранными поверхностями. В этом случае чем больше граней содержит вписанная поверхность, тем точнее ее развертка. Построенные таким образом развертки поверхностей называют приближенными.
Чтобы построить развертки неразвертывающихся поверхностей, эти поверхности разбивают на части, которые можно приближенно заменить развертывающимися поверхностями. После этого строят развертки этих частей, которые в сумме дают условную развертку неразвертывающейся поверхности.
§ 73. Развертки пирамидальных и конических поверхностей
При развертывании поверхности на плоскости каждой точке поверхности соответствует единственная точка на развертке: линия поверхности переходит в линию развертки; длины линий, величины плоских углов и площадей, ограниченных замкнутыми линиями, остаются неизмеренными. Таким образом, процесс построения развертки сводится к отыскиванию натуральной (истинной) величины каждого элемента поверхности и изображению их на плоскости.
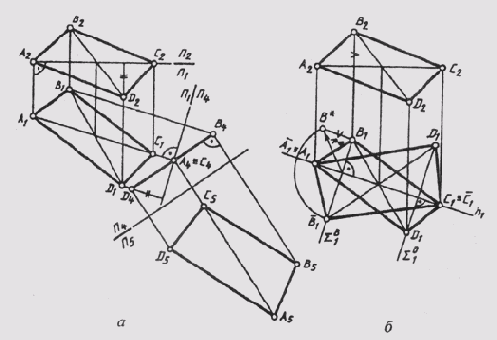
Рис. 146

Рис. 147
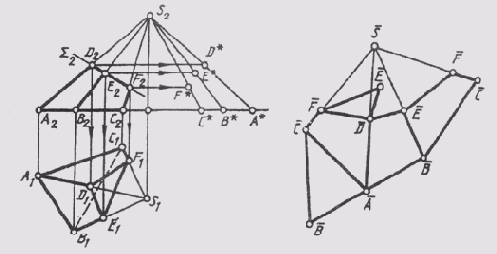
Рис. 148
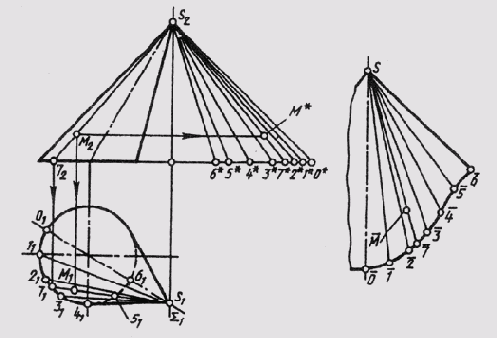
Рис.
149
Для нанесения на развертку точек D, Е и F, соответствующих вершинам сечения пирамиды плоскостью Sum, нужно определить истинные расстояния этих точек от вершины S. После построения развертки боковой грани поверхности усеченной части пирамиды нужно пристроить к ней треугольники АBС и DEF, дающие истинную величину основания и сечения пирамиды.
На рис. 149 способом триангуляции построена развертка конической поверхности, которая заменена поверхностью вписанной в нее двенадцатиугольной пирамиды. Развертка представляет собой симметричную фигуру, так как поверхность имеет плоскость симметрии Sum. В этой плоскости лежит самая короткая образующая S-6. По ней и сделан разрез поверхности. Самая длинная образующая S-0 является осью симметрии развертки поверхности.
Натуральные величины образующих определены с помощью прямоугольных треугольников, как в предыдущей задаче на рис. 149. От оси симметрии S-0 строим шесть в одну сторону и шесть в другую сторону примыкающих друг к другу треугольников с общей вершиной S. Каждый из треугольников строим по трем сторонам, при этом две сто-
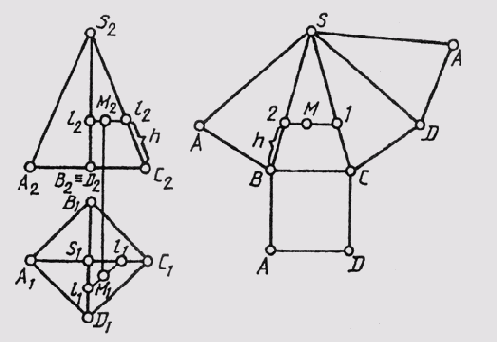
Рис.
150
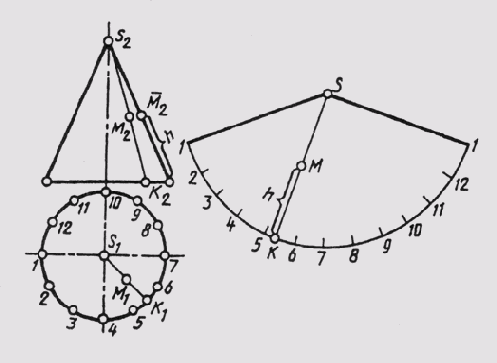
Рис.
151
§ 74. Развертки призматических и цилиндрических поверхностей
Развертки призматических и цилиндрических поверхностей строят способом нормального сечения. Поверхность рассекают плоскостью, перпендикулярной ее образующим (ребрам), и определяют истинную величину нормального сечения. Линию нормального сечения развертывают в прямую. Тогда образующие (ребра) поверхности при развертке ее на плоскость располагаются перпендикулярно развертке линии нормального сечения, которую принимают за базу отсчета размеров образующих (ребер).
На рис. 152 построена полная развертка поверхностей треугольной призмы ABCDEF. Так как боковые ребра призмы BE, AD и CF параллельны плоскости П2, то они в истинную длину изображены на фронтальной плоскости проекций. Плоскость нормального сечения Sum(Sum2) является фронтально проецирующей. Нормальное сечение POR призмы построено в натуральную величину на плоскости П4, параллельной плоскости Sum и перпендикулярной плоскости П2. Линию нормального сечения разворачиваем в прямую и через точки Р, Q, R, и Р проводим прямые, перпендикулярные развертке линии нормального сечения. На каждом из построенных перпендикуляров откладывают по обе стороны от линии Р Р отрезки боковых ребер, измеренные на плоскости П2 (до нормального сечения и после него). Отмечаем точки

Рис. 152
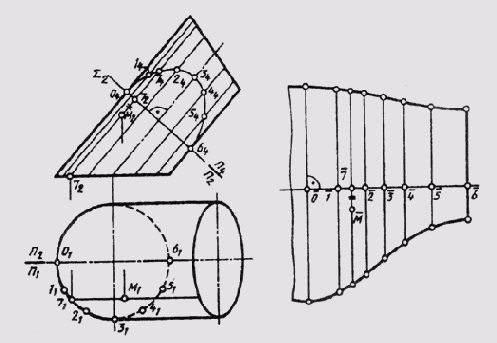
Рис.
153
На рис. 153 построена развертка боковой поверхности эллиптического цилиндра, в который для построения развертки вписана двенадцатиугольная призма. Поверхность имеет фронтальную плоскость симметрии. Самая длинная образующая — нулевая, самая короткая — шестая, по ней и сделан разрез поверхности. Развертка — фигура симметричная относительно нулевой образующей. Истинная величина половины нормального сечения поверхности плоскостью Sum построена на плоскости П4 — эллипс. Разворачиваем дугу полуэллипса в прямую 0 — 6с помощью хорд 04—14, ... 54 — 64, заменяющих кривые участки эллипса. В точках 0, 1, ... 6 на развертке восстанавливаем перпен-

Рис. 154
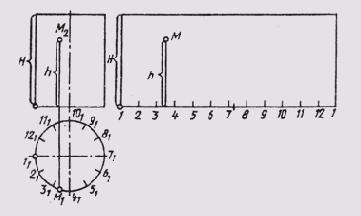
Рис.
155
С помощью седьмой образующей на развертку нанесена точка поверхности.
Построение разверток призматических и цилиндрических поверхностей значительно упрощается, если они представлены простыми прямыми фигурами. Для примера на рис. 154 приведена развертка трехгранной призы правильной формы. Развертки ее строим, воспользовавшись тем, что ребра ее АА, ВВ, СС параллельны фронтальной плоскости проекций и проецируются на нее в натуральную величину, а нижнее ABC и верхнее А'В'С' основания параллельны горизонтальной плоскости проекций и проецируются на нее в натуральную величину. Точка М на развертке трехгранной призмы строится обычным способом.
На рис. 155 приведен пример построения развертки прямого кругового цилиндра. Ее высота Н на фронтальную плоскость проекций проецируется в натуральную величину, а нижнее и верхнее основания параллельны горизонтальной плоскости проекций и на нее проецируются в натуральную величину. В этом случае развертку цилиндрической поверхности строим с помощью хорд, соединяющих соседние точки деления окружности оснований, в который вписан правильный двенадцатиугольник. В этом случае цилиндрическая поверхность условно заменена поверхностью вписанной правильной двенадцатигранной призмы, и развертка цилиндрической поверхности построена способом триангуляции.
Положение точки М на развертке цилиндрической поверхности определяется обычным способом.
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. Какие задачи называются метрическими?
2. Какие группы задач выделяются в метрических задачах?
3. Как на комплексном чертеже определить расстояние между двумя точками пространства; от точки до прямой; от точки до плоскости?
4. Как определить кратчайшее расстояние между двумя параллельными прямыми; скрещивающимися прямыми; от прямой до плоскости?
5. Какие построения необходимо выполнить на чертеже, чтобы определить натуральную величину угла между двумя пересекающимися прямыми общего положения?
6. Как по чертежу определить истинную величину угла между плоскостями общего положения, если ребро образованного ими двугранного угла не задано?
7. Какие вы знаете способы построения истинной величины фигуры сечения поверхности плоскостью общего положения?
8. Что называется разверткой поверхности?
9. Какие поверхности относятся к неразвертывающимся поверхностям?
10. Можно ли построить развертку неразвертывающейся поверхности?
11. Каким способом строят развертки пирамидальных (конических) поверхностей?
12. Каким способом строят развертки призматических (цилиндрических) поверхностей?
13. Как нанести на развертку поверхности точку, ей принадлежащую?