§ 60. Общие сведения о позиционных задачах

Задачи, связанные с решением вопросов взаимного расположения геометрических фигур на комплексном чертеже, называются позиционными.

Среди позиционных можно выделить две группы задач, представляющих наибольший практический интерес. К ним относятся задачи на взаимную принадлежность и задачи на взаимное перенесение. Задачи первой группы неоднократно упоминались при изучении глав 7 и 8. Это объясняется, тем, что любая линия есть производная точки, а любая поверхность есть производная линии. Конкретно вопросы принадлежности точки прямой рассмотрены в § 44, принадлежности точки и прямой плоскости в § 49, а принадлежности точки и линии поверхности в § 55.

Решение позиционных задач на принадлежность предполагает работу с линиями поверхности графически простыми, например прямой или окружностью. Это необходимо для того, чтобы не усложнять построений на комплексном чертеже. Для правильного выбора этих линий надо знать, какие семейства линий несет на себе та или иная поверхность.

Задачи

на взаимное пересечение связаны с построением точек, принадлежащих одновременно двум рассматриваемым геометрическим образам, например прямой и плоскости, двум плоскостям, плоскости и поверхности, двум поверхностям. Каждую из этих точек строят в пересечении двух вспомогательных линий. Эти линии должны быть графически простыми и принадлежать одной вспомогательной плоскости или поверхности. Выбор вспомогательных, поверхностей (посредников), несущих в себе вспомогательные линии, зависит от формы пересекающихся поверхностей. Совокупность построенных общих точек позволяет построить линию пересечения геометрических образов.

§ 61. Пересечение прямой с плоскостью

Прямая пересекает плоскость в одной точке. Точку пересечения прямой с плоскостью определяют путем построения вспомогательной прямой линии, лежащей в одной проецирующей плоскости с заданной прямой. На рис. 119, а приведен комплексный чертеж прямой l и плоскости 9 (ABC), причем т ~ Q (ABC). Через горизонтальную проекцию прямой l₁ проводим проекцию вспомогательной горизонтально проецирующей плоскости Sum₁. В пересечении плоскостей Q и Sum получаем линию т, то есть т =Sum ^ Q. Горизонтальная проекция прямой т определяется горизонтальными проекциями точек 1 и 2 пересечения линий ЕС и АС со вспомогательной плоскостью Sum , то есть В₁С₁ ^ Sum = l₁; А₁С₁ ^ Sum₁=2₁; т₁ = l₁^2₁.

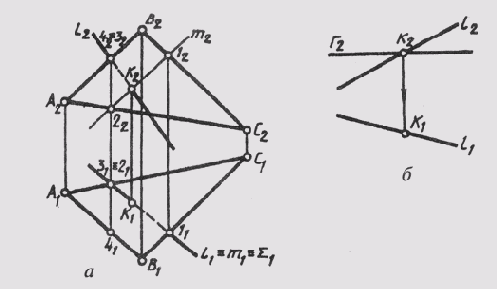
Рис. 119

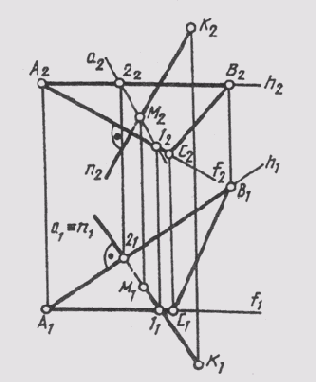
Рис. 120

Рис. 121

Для получения фронтальной проекции линии l построим фронтальные проекции точек 1 и 2, соединив которые, получим фронтальную проекцию m₂. В пересечении фронтальных проекций прямых т и l получим фронтальную проекцию точки К, принадлежащей и прямой l, и прямой т, лежащей в плоскости Sum. Значит, точка К и принадлежит плоскости Sum, и является точкой пересечения прямой l с плоскорью Sum.

Видимость прямой и плоскости относительно горизонтальной плоскости проекций определяется с помощью горизонтально конкурирующих точек 2 и 3, а видимость относительно фронтальной плоскости проекции — с помощью фронтально конкурирующих точек 3 и 4.

Если плоскость занимает частное положение, то одна проекция точки пересечения прямой с плоскостью определяется сразу в пересечении вырожденной проекции плоскости с соответствующей проекцией прямой (рис. 119, б).

Если прямая пересекает плоскость под прямым углом, то на комплексном чертеже проекции этой прямой располагаются перпендикулярно проекциям соответствующих линий уровня плоскости на основании теоремы о проецировании прямого угла (см. § 29).

На рис. 120 построены проекции основания М перпендикуляра п, проведенного к плоскости 9 (ABC) из точки К пространства. В AВС имеем: АВ — горизонталь (A₂B₂ _|_ A₂A₁), AC — фронталь (А₁С₁ _|_A₁A₂). Поэтому проекции перпендикуляра n э К располагаются: п₁ _|_A₁B₁ и n₂ _|_ А₂С₂. Основание перпендикуляра на плоскости построено с помощью вспомогательной линии а плоскости, лежащей в одной с перпендикуляром п горизонтально проецирующей плоскости (а ^ п = М).

Если прямая пересекает плоскость в бесконечности, то имеет место параллельность прямой с плоскостью. На рис. 121 построена прямая т, проходящая через точку N u параллельная плоскости треугольника KLM. На комплексном чертеже параллельность прямой и плоскости доказывается тем, что m₁ || а₁ и m₂ || а₂; a ~ KLM.

§ 62. Пересечение двух плоскостей

Две плоскости пересекаются по прямой линии. Для построения линии их пересечения необходимо найти две точки, принадлежащие этой линии. Задача упрощается, если одна из пересекающихся плоскостей занимает частное положение. В этом случае ее вырожденная проекция включает в себя проекцию линии пересечения плоскостей.

На рис. 122 приведен комплексный чертеж двух пересекающихся плоскостей £ и 0, причем плоскость Sum частного положения — фронтально проецирующая. Она пересекает линии АВ и АС плоскости 0, данной треугольниками ABC — плоскости общего положения. Точки пересечения 1 и 2 и определяют линию пересечения плоскостей. Соединив их, получаем искомую линию: a(1, 2) = Sum^Q.

Линию пересечения двух плоскостей, занимающих общее положение, можно построить в исходной системе плоскостей проекции. Для этого дважды решают задачу на построение прямой одной плоскости со второй плоскостью. Задачу можно решать в новой системе плоскостей проекции, построив изображение одной из пересекающихся плоскостей как плоскости проецирующей.

На рис. 123, а построена линия пересечения двух треугольников ABC и DEF путем построения точки М пересечения линии АВ с плоскостью DEF и точки N пересечения линии EF с плоскостью АВС:

1) АВ ~ Sum¹(Sum¹_|_П₂), Sum¹ ^DEF=l -2(1₂—2₂; 1₁—2₁), 1₁—2₁ ^ А₁B₁ = М_1, M₁,M₂ || А₁A₂,М₁М₂ ^ А₂В₂ = М₂,М(М,М₂);

Рис. 122

Рис. 123

2) EF ~ Sum²(Sum²_|_П₂), Sum² ^ ABC = 3—4(3₂—4₂; 3₁—4₁),3₁-4₁ ^ E₁F₁= = N₁, N₁N₂ || A₁,A₂; N₁N₂^ E₂F₂ = N₂; N(N₁,N₂);

3) M₁ U N₁, = M₁N₁, M₂ U N₂ = M₂N₂;

4) ABC^DEF = MN.

После построения определяют видимость пересекающихся плоскостей. На фронтальной плоскости она определена с помощью фронтально конкурирующих точек 1 и 5. Для определения видимости на горизонтальной плоскости проекций использованы горизонтально конкурирующие точки 6 и 7.

На рис. 123, б эта же линия пересечения построена с помощью дополнительных проекций данных плоскостей на плоскости П₄, относительно которой плоскость DEF занимает проецирующее положение. Дополнительные проекции построены из условия, что горизонталь h € DEF проецируется в точку на плоскости П₄ _|_ h. Новые линии связи проведены .через незаменяемые горизонтальные проекции точек А,

В, С, D, E, F параллельно h₁, а новая ось проекций П₁/П₄ _|_ h₁. Замеренные на плоскости П₂ высоты точек определили их проекции на плоскости П₄.

A₄B₄C₄^ D₄E₄F₄ = M₄K₄, так как А₄В₄ ^ D₄E₄F₄ = М₄ и В₄С₄ ^ D₄E₄F₄ = = К₄. По направлению новых линий связи определяем горизонтальную проекцию линии МК (М₁К₁). Отмечаем точку пересечения стороны EF c линией МК: E₁F₁ ^ M₁K₁ = N₁. Точки отрезка NK не имеют общих точек с плоскостью DEF.

Пересекающиеся плоскости в частном случае могут быть перпендикулярными. Для выявления случаев перпендикулярности надо помнить, что если две плоскости взаимно перпендикулярны, то одна из них проходит через перпендикуляр к другой плоскости. На рис. 122 дан комплексный чертеж взаимно перпендикулярных пересекающихся плоскостей: одна фронтально проецирующая Sum (Sum₂), а вторая — общего положения (ABC) — содержит в себе перпендикуляр АВ к плоскости Sum(AB||П₂; A₂B₂Sum₂).

Две плоскости в общем случае могут пересекаться в бесконечности. Тогда имеет место параллельность этих плоскостей. При выявлении этого случая следует учитывать, что у параллельных плоскостей две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости. На рис. 91 плоскость S параллельна плоскости Sum₂, так как а || с, b || d.

§ 63. Пересечение поверхности с плоскостью. Тела с вырезами

При пересечении поверхности с плоскостью в сечении получают плоскую линию. Эту линию строят по отдельным точкам. В начале построения сперва выявляют и строят опорные точки, лежащие на контурных линиях поверхности, а также точки на ребрах и линиях основания поверхности. В тех случаях, когда проекция линии пересечения не полностью определяется этими точками, строят дополнительные, промежуточные точки, расположенные между опорными.

В данном разделе рассматриваются случаи пересечения поверхности плоскостями частного положения, так как в случае наличия секущей плоскости общего положения чертеж всегда можно преобразовать так, чтобы секущая плоскость стала проецирующей (см. рис. 129).

В случае пересечения гранной поверхности плоскостью получается плоская ломаная линия. Чтобы построить эту линию, достаточно определить точки пересечения плоскостью ребер и сторон основания, если имеет место пересечение основания, и соединить построенные точки с учетом их видимости (рис. 124, а). Так как в этом случае секущая плоскость Е занимает фронтальное проецирующее положение, то точки пересечения ребер определяются без дополнительных построений:

AS^Sum=1(1₂; l₁); Sum = (2₂; 2₁); CS^Sum = 3(3₂; 3₁).

Так как грань ACS относительно плоскости П\ невидима, то и линия l₁—3₁ тоже невидима.

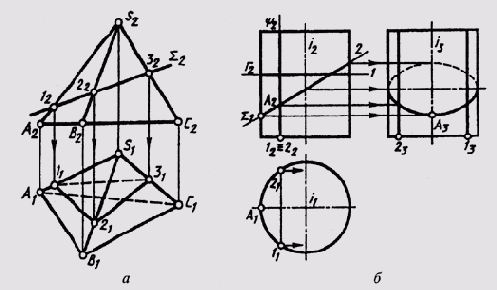
Рис. 124

В случае пересечения цилиндрической поверхности вращения плоскостью могут быть получены следующие линии (рис. 124, б):

окружность, если секущая плоскость Г перпендикулярна оси вращения поверхности;

эллипс, если секущая плоскостьSum не перпендикулярна и не параллельна оси вращения;

две образующие прямые, если секущая плоскость U параллельна оси поверхности.

На плоскость П₁, перпендикулярную оси вращения поверхности, окружность и эллипс на поверхности цилиндра проецируются в окружность, совпадающую с проекцией всей поверхности.

При пересечении конической поверхности вращения плоскостью могут быть получены следующие линии (рис. 125, а — д):

окружность, если секущая плоскость Г перпендикулярна оси вращения (а);

эллипс, если секущая плоскость Sum¹ пересекает все образующие поверхности (б);

парабола, если секущая плоскость (Sum²) параллельна только одной образующей (S— 1) поверхности (в);

гипербола, если секущая плоскость (Sum³) параллельна двум образующим (S—5 и 5—6) поверхности (г);

две образующие (прямые), если секущая плоскость (Sum⁴) проходит через вершину S поверхности (д). Проекции кривых линий сечений

Рис. 125

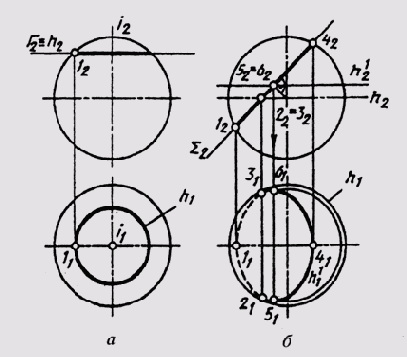
Рис. 126

плоскостью конуса строятся по отдельным точкам (точки 2, 4 на рис. 125, б).

При пересечении сферы плоскостью всегда получается окружность. Если секущая плоскость параллельна какой-либо плоскости проекций, то на эту плоскость окружность сечения проецируется без искажения (рис. 126, а). Если секущая плоскость занимает проецирующее положение, то на плоскости проекций, которой секущая плоскость перпендикулярна (рис. 126, б—на фронтальной), окружность сечения изображается отрезком прямой (1₂—4₂), длина которого равна диаметру окружности, а на другой плоскости — эллипсом, большая ось которого (5₁—6₁) равна диаметру окружности сечения. Этот эллипс строят по точкам. Точки видимости 2 и 3 относительно плоскости П₁ лежат на экваторе сферы.

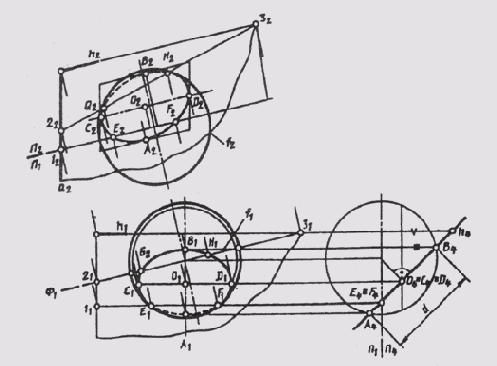
Рис. 127

Задача построения линии пересечения несколько сложнее при пересечении сферы плоскостью общего положения (рис. 127) Q(a^h).

Этот случай можно свести к предыдущему (см. рис. 126, б), если построить дополнительные изображения сферы и секущей плоскости на плоскости П₄ _|_П₁, причем П₄ _|_h (6). Тогда плоскость в станет проецирующей Q _|_П₄ в новой системе плоскостей (см. рис. 127). На чертеже оси проекции проходят через центр сферы. На плоскости П₄ отмечаем проекции опорных точек: А₄ — самой низкой точки сечения; В₄ — самой высокой, дающих величину диаметра d окружности сечения с центром в точке О (О₄); Е₄ = F₄ — на экваторе сферы— точек видимости линии сечения относительно плоскости П₁, С₄ = D₄ = O₄ — горизонтального диаметра CD, определяющего большую ось эллипса, — горизонтальной проекции окружности сечения. Горизонтальная проекция сечения — эллипс — легко строится по большой C₁D₁ и малой А₁В₁ осям. Фронтальная проекция окружности тоже эллипс, который можно построить по сопряженным диаметрам A₂B₂ и C₂D₂ (высоты этих точек отмечены на плоскости П₂ и на плоскости П₄) с помощью описанного параллелограмма. Видимость окружности сечения относительно плоскости П₂ определяется точками G и H, полученными в пересечении главного меридиана сферы f с плоскостью 9. Для этого взята вспомогательная плоскость уровня Ф:

Ф э f; Ф ^ Q = 2—3;

f₂^2₂—3₂ = H₂ и G₂.

Линии среза получаются при пересечении поверхности вращения плоскостью, параллельной оси вращения поверхности. Линии среза часто встречаются на поверхностях деталей. На рис. 128 построена линия среза комплексной поверхности, состоящей из поверхностей сферы и конуса, фронтальной плоскостью уровня Ф. Линия среза включает ли-

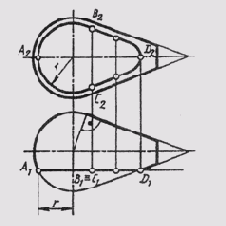
Рис. 128

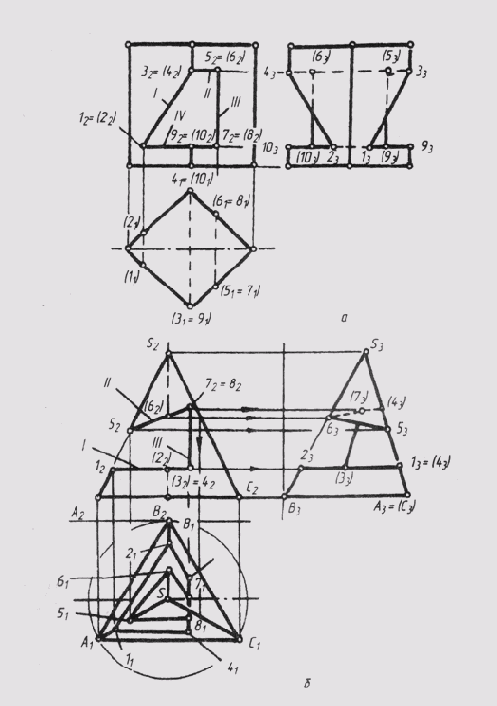
Рис. 129

нию пересечения сферы (В₂ —А₂ — С₂) — часть окружности радиуса r — и линию пересечения конуса (В₂ — D₂ — С₂) — ветвь гиперболы, которую строят по отдельным точкам. В качестве вспомогательных секущих плоскостей для построения промежуточных точек берут плоскости, перпендикулярные оси вращения поверхностей.

Пересечение поверхностей геометрических фигур может быть осуществлено не одной, а несколькими секущими плоскостями. Как и в случае пересечения одной плоскостью, построение каждой линии пересечения упрощается, если секущие плоскости являются плоскостями частного положения.

На рис. 129, а по заданной фронтальной проекции выреза, выполненного в правильной треугольной пирамиде тремя фронтально-проецирующими плоскостями, построены горизонтальная и профильная проекции. При решении таких задач вначале анализируют форму каждой грани выреза. Сторонами этих многоугольников будут: 1) линии пересечения граней пирамиды с плоскостями выреза и 2) линии пересечения плоскостей выреза друг с другом. Вершинами: 1) точки пересечения ребер пирамиды с плоскостями выреза и 2) концы отрезков, по которым грани выреза пересекаются друг с другом. На рис. 129, а плоскость I пересекает ребра пирамиды SА и SВ в точках 1 и 2, а с плоскостью III пересекается по отрезку 3—4; таким образом, форма грани 1 — четырехугольник 1—2—3—4. Аналогично в плоскости II получается четырехугольник 5—6—7—8. Вершинами четырехугольника 3—4—8—7 в грани III являются концы отрезков, по которым эта грань пересекается с гранями I и П. Стороны всех этих многоугольников составляют очертания выреза. Для получения их проекций на пл. П₁ и П₃ сначала нужно отметить фронтальные проекции (1₂ . . . 8₂) всех вершин, затем построить горизонтальные и профильные их проекции, после чего соединить на П₁ и П₃ вершины каждого многоугольника последовательно, с учетом видимости каждого отрезка. Грань I расположена горизонтально, поэтому на П₃ проецируется в горизонтальный отрезок. Грань пирамиды SAC профильно-проецирующая, поэтому все линии выреза, полученные в ней, на П₃ проецируются в одну линию. При обводке чертежа нужно стереть или оставить тонкими линиями части вырезаемых ребер пирамиды.

На рис. 129, б построены проекции правильной четырехугольной призмы с отверстием, ограниченным фронтально-проецирующими плоскостями.

Каждая грань выреза (I, II, III, IV) представляет собой плоский многоугольник, сторонами которого являются: 1) линии пересечения соответствующей секущей плоскости с гранями призмы и 2) линии пересечения плоскостей выреза друг с другом (отрезки 1—2; 3—4; 5—6; 7—8). Исходя из этого, имеем: грань I — трапеция 1—2—4—3; грань II — трапеция 3—4—6—5; грань III — прямоугольник 5—6—8—7; грань IV — шестиугольник 1—2—10—8—7—9. После анализа формы граней выреза производится построение проекций этих фигур на пл. П₁ и П₃. На пл. П₁ все линии контура совпадают с вырожденными проекциями соответствующих граней. Грани II и IV расположены горизонтально, поэтому на пл. П₃ проецируются в виде горизонтальных отрезков.

Рис. 130

На рис. 130, а показано построение выреза в цилиндре. Вырез ограничен тремя гранями. Вертикальная грань ограничена двумя горизонтальными сквозными ребрами 55' и 66' и прямыми 5,6 и 5' 6' на боковой поверхности цилиндра. Наклонную грань ограничивают частью эллипса на боковой поверхности цилиндра и сквозным ребром 55'. Горизонтальная грань представляет собой плоскую фигуру, ограниченную частью окружности и прямой 66'.

Линии выреза, лежащие на боковой поверхности цилиндра, проецируются на окружность основания на П₁. Профильная их проекция строится по точкам измерения их глубин относительно плоскости симметрии цилиндра ф. Сквозные ребра 55' и 66' невидимы на П₁ и П₃

На рис. 130, б приведена задача построения выреза в конусе. Призматическое отверстие в конусе имеет три внутренние стенки, границами между которыми служат ребра АА', BE' и СС', которые перпендикулярны П2i. Правая стенка (АЕ) имеет форму трапеции, так как секущая плоскость этой стенки проходит через вершину S и пересекает конус по образующим SD и SD'. Части этих образующих между точками А (А') и В (В¹) дают контур правой стенки. Нижняя стенка (между ребрами ВВ' и СС') представляет собой часть круга, ограниченного параллельно h. Левая стенка (между ребрами АА' и СС') ограничена частью параболы, проекции которой определяются точками F (Р) на профильном меридиане конуса и промежуточными точками К (К') на вспомогательной параллели h'.

Профильный меридиан конуса «вырезан» на участке между точками Е (E') и F (F).

На рис. 130, в построены проекции сферы с вырезом. Призматическое отверстие имеет 4 внутренние стенки, границами между которыми служат ребра АА', ВВ', СС', DD', которые перпендикулярны П₂.

Каждая стенка представляет собой часть круга. Верхняя и нижняя параллельны П₁ и проецируются на нее в виде части окружности с радиусами, которые определяются по параллелям h и h'.

Экватор вырезан между точками 1,5 и 2,6. Правая и левая стенки выреза параллельны П₃ и проецируются на нее в виде частей круга с радиусами, которые определяются окружностями Р и Р'. Профильный меридиан вырезан между точками 3,7 и 4,8.

Приведенные примеры показывают, что, меняя положение секущих плоскостей, можно получить вырезы заданной формы.

§ 64. Пересечение поверхностей

При пересечении двух поверхностей образуется линия, в общем виде представляющая собой пространственную кривую, которая может распадаться на две части и более. Причем полученные части могут быть и плоскими, и кривыми.

Если пересекаются гранные поверхности, в общем случае получается пространственная ломаная кривая.

Линию пересечения двух плоскостей строят по отдельным точкам. Сначала в пересечении контурных линий одной поверхности с другой определяют и строят опорные точки. Построение этих точек позволяет видеть, в каких пределах расположены проекции линии пересечения и где между ними имеет смысл построить промежуточные (или случайные) точки. При построении точек пересечения двух поверхностей следует помнить, что проекции этих линий всегда располагаются в пределах площади наложения одноименных проекций пересекающихся плоскостей. На рис. 131 изображены две пересекающиеся поверхности. Площадь сечения — заштрихована. В пределах этой площади и будет расположена линия пересечения заданных поверхностей на данной плоскости проекций.

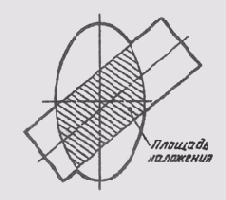
Рис. 131

Общим способом построения точек линии пересечения двух поверхностей является способ вспомогательных поверхностей — посредников. Посредники пересекают заданные поверхности по линиям, желательно по графически простым. Тогда в пересечении этих линий получаются точки, принадлежащие обеим поверхностям, а значит, и линии их пересечения. В качестве поверхностей-посредников используют или плоскости, или сферы. В зависимости от принятого вида посредника именуют и способ построения линии пересечения: способ вспомогательных секущих плоскостей или способ вспомогательных сфер.

§ 65. Построение линии пересечения поверхностей способом вспомогательных секущих плоскостей

При построении линии пересечения двух поверхностей способом вспомогательных секущих плоскостей секущие плоскости, принятые в качестве посредников, могут быть и общего, и частного положения. Более широкое применение находят плоскости частного положения.

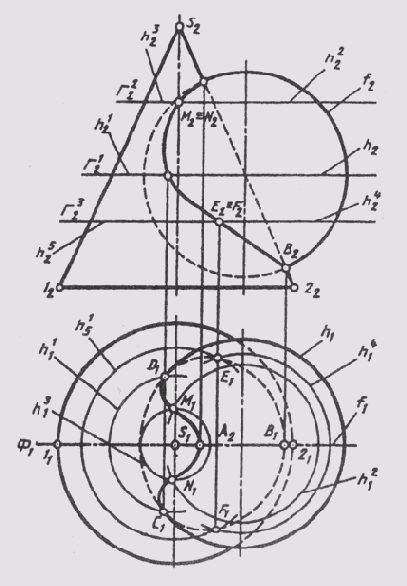
Рис. 132

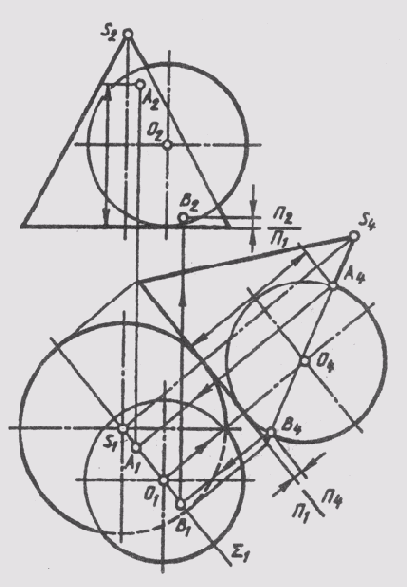
Рис. 133

Плоскости общего положения применяются в ограниченных случаях. Например, их удобно использовать при построении линии пересечения конических и цилиндрических, а также пирамидальных и призматических поверхностей общего вида, когда основания этих поверхностей расположены в одной и той же плоскости.

Решение задачи построения линии пересечения двух поверхностей способом вспомогательных секущих плоскостей рассмотрим на примере пересечения конуса вращения со сферой. В качестве поверхностей-посредников примем плоскости частного положения— горизонтального уровня. На рис. 132 сначала отметим очевидные общие точки А и В поверхностей в пересечении их главных меридианов f и 1-S-2, так как поверхности имеют общую фронтальную плоскость симметрии Ф(Ф₁); f₂^S₂—S₂ = А₂(В₂); A₂A_l(B₂B_l) || S₂S₁, A₂A_l(B₂B_l) ^f₁ =A₁(B₁)

Эти опорные точки являются наивысшей А и наинизшей В точками линии пересечения, а также точками видимости линии на плоскости П₂.

Брать вспомогательные фронтальные плоскости, параллельные П₂, для построения следующих точек неудобно, так как они будут пересекать конус по гиперболам. Графические простые линии (окружности параллелей) на данных поверхностях получаются от пересечения их горизонтальными плоскостями уровня Г.

Первую такую вспомогательную плоскость Г¹ берем на уровне экватора сферы И. Эта плоскость пересекает конус по параллели h¹. В пересечении этих параллелей находятся точки видимости линии пересечения относительно плоскости П¹:

h¹^h¹₁ = С₁(D₁); С₁С₂|| S₁S₂; С₁С₂ ^ h₂(h^l₂) = C₂(D₂).

Если пересекающиеся поверхности вращения не имеют общей фронтальной плоскости симметрии (рис. 133), то самую высокую А и низкую В точки линии пересечения поверхности легко определить, построив изображения этих поверхностей на плоскости П₄, параллельной осевой плоскости Sum (Sum₁) данных поверхностей. Можно построить проекции всей линии пересечения в системе плоскостей П₁_|_П₄, а затем построить ее фронтальную проекцию в проекционной связи с горизонтальной проекцией, замеряя высоты точек на плоскости П₄, так, как это показано на рис. 132 для точек А и В.

§ 66. Построение линии пересечения поверхностей способом вспомогательных сфер

При построении линии пересечения поверхностей особенности пересечения соосных поверхностей вращения позволяют в качестве вспомогательных поверхностей-посредников использовать сферы, со-осные с данными поверхностями.

К соосным поверхностям вращения относятся поверхности, имеющие общую ось вращения. На рис. 134 изображены соосные цилиндр и сфера (рис. 134, а), соосные конус и сфера (рис. 134, б) и соосные цилиндр и конус (рис. 134, в).

Соосные поверхности вращения всегда пересекаются по окружностям, плоскости которых перпендикулярны оси вращения. Этих общих для обеих поверхностей окружностей столько, сколько существует точек пересечения очерковых линий поверхностей. Поверхности на рис. 134 пересекаются по окружностям, создаваемым точками 1 и 2 пересечения их главных меридианов.

Вспомогательная сфера-посредник пересекает каждую из заданных поверхностей по окружности, в пересечении которых получаются точки, принадлежащие и другой поверхности, а значит, и линии пересечения.

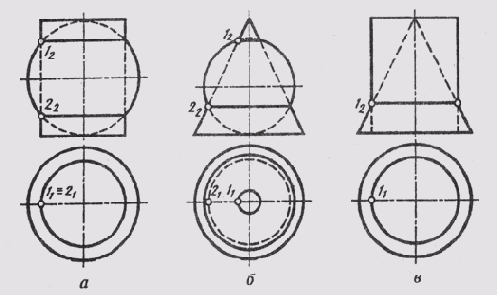
Рис. 134

Если оси поверхностей пересекаются, то вспомогательные сферы проводят из одного центра-точки пересечения осей. Линию пересечения поверхностей в этом случае строят способом вспомогательных концентрических сфер.

При построении линии пересечения поверхностей для использования способа вспомогательных концентрических сфер необходимо выполнение следующих условий:

1) пересечение поверхностей вращения;

2) оси поверхностей — пересекающиеся прямые — параллельны одной из плоскостей проекций, т. е. имеется общая плоскость симметрии;

3) нельзя использовать способ вспомогательных секущих плоскостей, так как они не дают графически простых линий на поверхностях.

Обычно способ вспомогательных сфер используется в сочетании со способом вспомогательных секущих плоскостей. На рис. 135 построена линия пересечения двух конических поверхностей вращения с пересекающимися во фронтальной плоскости уровня Ф (Ф₁) осями вращения. Значит, главные меридианы этих поверхностей пересекаются и дают в своем пересечении точки видимости линии пересечения относительно плоскости П₂ или самую высокую А и самую низкую В точки. В пересечении горизонтального меридиана h и параллели h', лежащих в одной вспомогательной секущей плоскости Г(Г₂), определены точки видимости С и D линии пересечения относительно плоскости П₁. Использовать вспомогательные секущие плоскости для построения дополнительных точек линии пересечения нецелесообразно, так как плоскости, параллельные Ф, будут пересекать обе поверхности по гиперболам, а плоскости, параллельные Г, будут давать в пересечении поверхностей окружности и гиперболы. Вспомогательные горизонтально или фронтально проецирующие плоскости, проведенные через вершину одной из поверхностей, будут пересекать их по образующим и эллипсам. В данном примере выполнены условия, позволяющие применение вспомогательных сфер для построения точек линии пересечения. Оси поверхностей вращения пересекаются в точке О (О₁; О₂), которая является центром вспомогательных сфер, радиус сферы изменяется в пределах

Rmin < R < Rmах- Радиус максимальной сферы определяется расстоянием от центра О наиболее удаленной точки В (R_max = О₂В₂), а радиус минимальной сферы определяется как радиус сферы, касающейся одной поверхности (по окружности h²) и пересекающей другую (по окружности h³).

Плоскости этих окружностей перпендикулярны осям вращения поверхностей. В пересечении этих окружностей получаем точки Е и F, принадлежащие линии пересечения поверхностей:

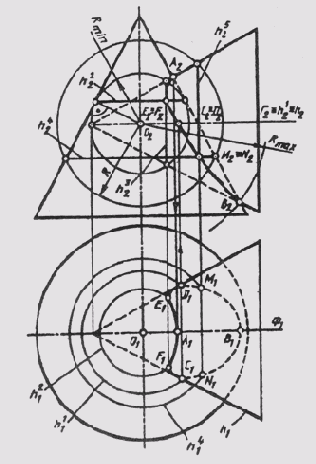
Рис. 135

h²₂ ^ h³₂ = E₂(F₂); Е₂Е₁ || А₂А₁;

Е₂Е₁ ^ h²₁ =E₁; F₂F ^ h₁ = F₁

Промежуточная сфера радиуса R пересекает поверхности по окружностям h⁴ и h⁵, в пересечении которых находятся точки Ми N:

h⁴₂ ^ h⁵₂ = M₂(N₂); M₂M₁ || А₂А₁,

М₂М₁ ^ h⁴₁ = М₁; N₂N₁ ^ h⁴₁ = N₁

Соединяя одноименные проекции построенных точек с учетом их видимости, получаем проекции линии пересечения поверхностей.

§ 67. Особые случаи построения линии пересечения двух поверхностей вращения

При построении линии пересечения поверхностей вращения — конуса и цилиндра — могут быть различные случаи. На рис. 136 изображены три случая пересечения цилиндра и конуса вращения. В первом случае (рис. 136, а) цилиндр врезается в конус, потому что если вписать в конус сферу с центром в точке пересечения осей поверхностей, то радиус ее будет больше радиуса цилиндра. Все образующие цилиндра пересекаются с поверхностью конуса. Во втором (рис. 136, б) конус врезается в цилиндр, так как сфера, вписанная в цилиндр, пересекает конус. Все образующие конуса пересекают поверхность цилиндра. В третьем (рис. 136, в) сфера, вписанная в одну поверхность, касается второй поверхности, и в пересечении участвуют все образующие и цилиндра, и конуса. В этом случае пространственная линия пересечения поверхностей распадается на две плоские кривые (эллипсы).

Это положение подтверждается теоремой Монжа: если две поверхности второго порядка описаны вокруг третьей поверхности второго порядка, то они пересекаются по двум кривым второго порядка. Такие поверхности имеют две точки, в которых они касаются друг друга, или говорят, что поверхности имеют двойное прикосновение. Линия пересечения двух поверхностей вращения, имеющих двойное прикосновение, распадается на две кривые второго порядка, плоскости которых проходят через прямую, соединяющую точки прикосновения (рис. 137). Две цилиндрические поверхности вращения одного диаметра касаются друг друга в точках А и В или имеют общие касательные, плоскости Ф¹ и Ф². Линия АВ занимает фронтально проецирующее положение, поэтому плоскости кривых пересечения будут фронтально проецирующими. Эллипсы ACBF и AEBD изображаются

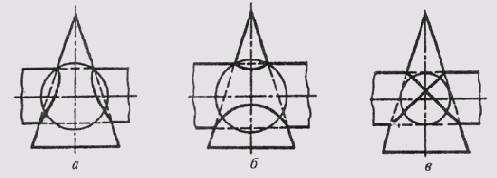
Рис. 136

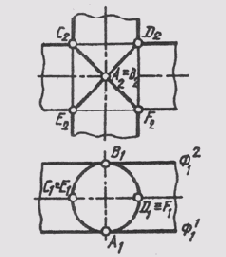
Рис. 137

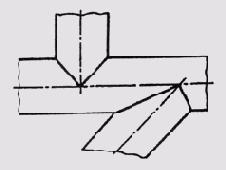
Рис. 138

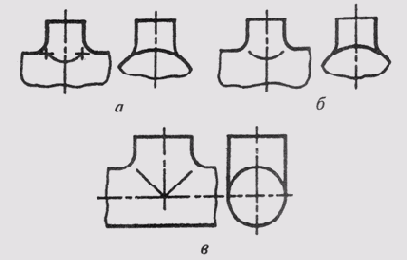
Рис. 139

отрезками прямых на фронтальной плоскости проекций и окружностями, совпадающими с вырожденной проекций вертикального цилиндра, на горизонтальной плоскости проекций. Это положение широко используется при изображении пересекающихся труб или отверстий одного диаметра (рис. 138).

В конструкциях технических деталей часто при пересечении поверхностей вращения используют сопрягающую поверхность, которая осуществляет плавный переход от одной поверхности к другой (рис. 139, а, б, в).

Чтобы не строить две близко расположенные линии пересечения сопрягающей поверхности с основными поверхностями, на чертеже проводят условно одну линию, выполняя ее тонкой сплошной линией.

Эту линию и называют линией перехода. Линия перехода заканчивается в точках пересечения очерковых линий основных поверхностей (рис. 139, а) и заменяется более простыми (циркульными) кривыми.

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

1. Какие задачи называются позиционными?

2. Какова последовательность решения задач на пересечение на комплексном чертеже?

3. Какая прямая является линией пересечения плоскости общего положения с горизонтальной плоскостью уровня?

4. Какая прямая является линией пересечения плоскости общего положения с фронтально проецирующей плоскостью?

5. По какой линии пересекаются две фронтально проецирующие плоскости?

6. Как определяется видимость при пересечении двух плоскостей общего положения?

7. Как строится линия пересечения поверхностей плоскостью?

8. Какие линии могут быть получены в сечении прямого кругового цилиндра, конуса, сферы?

9. Что такое линия среза?

10. Что представляет собой вырез?

11. Чем можно задать необходимую форму выреза?

12. Как строят линию пересечения двух поверхностей?

13. Какие вспомогательные поверхности удобно использовать при построении точек линии пересечения двух поверхностей?

14. В чем сущность способа вспомогательных секущих плоскостей в построении линии пересечения двух поверхностей?

15. По каким линиям пересекаются соосные поверхности вращения?

16. Когда можно использовать вспомогательные сферы при построении линии пересечения двух поверхностей?

17. По каким линиям пересекаются два прямых круговых цилиндра одного диаметра, если их оси пересекаются? Почему?

18. Какую линию называют линией перехода и как она вычеркивается при изображении пересекающихся поверхностей?

---

---